誤差指標¶
Eureqa誤差指標は、Eureqaモデルがデータにどれだけ適切に適合するかを測定します。 DataRobotでEureqaモデルのチューニングを実行すると、誤差と複雑さを最適化したモデルが検索されます。 適切な適合を最も適切に定義する誤差指標は、データの本質およびモデリングの目的によって異なります。 DataRobotは、Eureqaモデルのさまざまな誤差指標をサポートします。
誤差指標の選択および設定によって、DataRobotで解の品質を評価する方法が決定されます。 各モデルにデフォルトの誤差指標が設定されますが、上級ユーザーは別の誤差指標を最適化することができます。 誤差指標の設定を変更すると、解の最適化方法が変化します。
誤差指標パラメーターerror_metricは予測モデルのパラメーター内で使用でき、Eureqaモデルのチューニングの一環として変更できます。 以下に使用可能な誤差指標の一覧を示します。
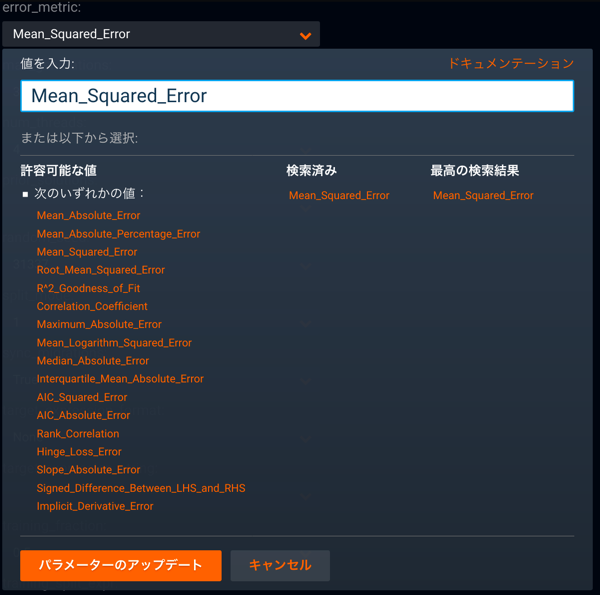
DataRobot対Eureqa¶
備考
DataRobotの最適化指標とEureqaの誤差指標には、いくつかの類似点があります。 しかし、指標式が別の形で表現される場合があります。 たとえば、予測がy^と表される場合とf(x)と表される場合があります。 これは両方とも正しい表示で、ニュアンスとして、y^は過程にかかわらず一般的な予測を示すことがあり、f(x)は基となる方程式を表すことのある関数を示します。
DataRobotでは、プロジェクトレベルで誤差指標を設定する最適化指標を使用できます。 最適化指標は、すべてのモデル(Eureqaを含む)のリーダーボードエントリに示される誤差値の評価、複数の異なるモデルの比較、およびリーダーボードのソートに使用します。
一方、Eureqaの誤差指標はプロジェクトレベルの設定ではなく、関連する解に対するEureqaアルゴリズムの最適化方法を制御します。 これらの指標を設定するときは、これらの指標が完全に独立していること、および一般的にいずれかの指標を設定してももう一方の指標には影響しないことに注意してください。
Eureqa誤差指標の選択¶
問題に対する最適な誤差指標は、使用するデータおよびモデリング分析の目的によって異なります。 多くの問題において正しい1つの答は存在しないので、いくつかの異なる誤差指標でモデルを実行し、どのようなタイプのモデルが生成されるかを確認し、どの結果がモデリング目標に最も一致しているかをチェックすることをお勧めします。
誤差指標を選択する際は、誤差指標の設定および構成に関する推奨事項を参照してください。
エラー指標パラメーター¶
平均絶対値¶
残差の絶対値の平均。 値が小さいほど誤差が低くなります。
詳細:平均絶対誤差は次のように計算されます。
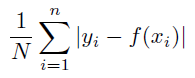
使用目的:残差誤差の最小化。 平均絶対誤差は優れた汎用誤差指標です。平均平方誤差に似ていますが、外れ値に対する許容度が平均平方誤差よりも高いです。 これは、時系列分析の予測誤差の一般的な指標です。 この指標の値は、平均距離予測が実測値からのものであるとして解釈できます。
注意事項:
- ノイズは、二重指数分布に従うと仮定されます。
- 平均平方誤差(MSE)に比べて、平均絶対誤差は外れ値に対して寛容になる傾向があります。MSEで最適化すると外れ値の加重が大きすぎる場合に、MAEは適切な選択です。
- モデル予測値と実測値の間の平均誤差として解釈できます。
平均絶対パーセンテージ¶
絶対パーセント誤差の平均。 値が小さいほど誤差が低くなります。 ターゲット特徴量 = 0の実測値の行が誤差の計算から除外されることに注意してください。
詳細:平均絶対パーセント誤差は次のように計算されます。
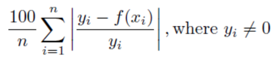
使用目的:絶対パーセント誤差の最小化。 平均絶対パーセント誤差(MAPE)は時系列予測分析の予測誤差の一般的な指標です。 この指標の値は、予測値が実測値と異なる平均パーセントとして解釈できます。
注意事項:
- 実測値が0の場合、平均絶対パーセント誤差は定義されません。 Eureqaの計算では、実測値が0の行は除外されます。
- 平均絶対パーセント誤差は非常に小さい実測値に対して極度に敏感です。小さい値の高いパーセント誤差によって誤差指標計算が左右されることがあります。
- 予測値と実測値との違いの平均パーセントとして解釈できます。
- 平均絶対パーセント誤差によってモデルにバイアスが生じ、実測値が過小評価されることがあります。
平均二乗¶
残差の二乗値の平均。 値が小さいほど誤差が低くなります。
詳細:平均平方誤差は次のように計算されます。
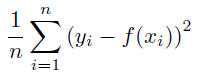
使用目的:平方残差誤差の最小化。 平均平方誤差は最も一般的な誤差指標です。 極端な誤差が重視されるので、大きな誤差の重大性が懸念される場合に便利です。
注意事項:
- ノイズは正規分布に従うと仮定されます。
- 小さい逸脱に対する許容度が高く、外れ値に敏感です。
- 分類問題の場合、平均平方誤差に最適化されたロジスティックモデルは、予測確率として解釈できる値を生成します。
- 平均平方誤差に最適化することは、R^2に最適化することと同等です。
二乗平均平方根¶
残差の二乗値の平均。 値が小さいほど誤差が低くなります。
詳細:二乗平均平方根誤差は次のように計算されます。
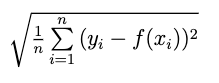
使用目的:平方残差誤差の最小化。 二乗平均平方根誤差は平均平方誤差と同様に使用されます。 二乗平均平方根誤差は平均平方誤差に比べて極端な誤差が重視されないので外れ値による影響は少なくなりますが、レコードの数が多いモデルが高く評価され、少ないモデルが低く評価される傾向があります。
注意事項:
- ノイズは正規分布に従うと仮定されます。
R^2適合度(R^2)¶
モデルで説明できるターゲット特徴量内の逸脱のパーセント。 値が高いほど高い適合性を示します。
詳細:R^2は次のように計算されます。
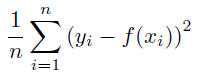
説明された分散の割合。 説明された分散のパーセントを取得するために、この値に100が乗算されます。
SStotは総分散に比例し、SSresは平方の残差二乗和です(説明されない分散に比例)。
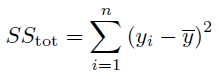
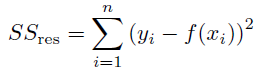
使用目的:説明された分散の最大化。 これは、数値がパーセントとしてレポートされる点を除き、平均平方誤差の最適化と同等です。 これは優れたデフォルトの誤差指標です。 平均平方誤差と同様に、R^2は小さい誤差よりも大きい誤差にペナルティを科すので、大きな誤差の重大性が懸念される場合に便利です。
注意事項:
- ノイズは正規分布に従うと仮定されます。
- データのスケールに関係なく、解釈は同じです。
- R^2が負の値である場合、モデルが信号を取得していないこと、モデルがシンプルすぎること、または予測に適していないことが示唆されています。
- R^2への最適化は、平均平方誤差への最適化と同等です。
- R^2は相関係数の2乗に密接に関係します。
相関係数¶
モデルによって生成された予測と実測ターゲット値が線形関係性にどれだけ近いかを測定します。 大きい値は強いPositive相関を示します。0は相関がないことを示し、1は完全なPositive相関を表します。-1は完全なNegative相関を表します。
詳細:相関係数は次のように測定されます。
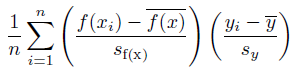
ここで、sf(x)およびsyはモデルおよびターゲット特徴量の未修正のサンプル標準偏差です。
使用目的:正規化共分散の最大化。 データの形状を説明するパターンを見つけることを目的とした特徴量の探索で一般的に使用される誤差指標。 モデルでデータのスケールとオフセットを探索する必要がないので、最適化の速度が他の指標よりも速くなります。
注意事項:
- 誤差の大きさとオフセットは無視されます。 したがって、相関係数だけに最適化されたモデルではターゲット特徴量と同じ形状に適合しようとしますが、実際の予測値は実測値に近くないことがあります。
- データのスケールに関係なく、値は常に [-1, 1] のスケール内です。
- 1は完全な正の相関で、0は相関なし、そして-1は完全な逆相関です。
最大絶対値¶
最大の絶対誤差の値。 値が小さいほどモデルは優れています。
詳細:最大絶対誤差は次のように計算されます。
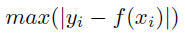
使用方法:最大誤差の最小化。 この指標は、単一の最も大きい誤差だけに注目し、シンボリックな単純化などの正確な適合を求める場合に使用します。 一般的に、データ内にノイズがない場合に使用されます(処理済みデータ、シミュレートされたデータ、または生成されたデータなど)。
注意事項:
- モデル全体の評価は単一のデータポイントに依存します。
- 入力データにノイズがほどんどないか皆無の場合に最適です。
平均対数平方¶
平方残差の対数の平均。 値が小さいほど誤差が低くなります。
詳細:平均対数平方誤差は次のように計算されます。
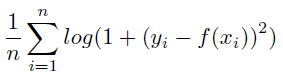
ここで、logは自然対数です。
使用目的:平方対数誤差の最小化。 大きい誤差の影響を削減するので、モデルの作成において外れ値の影響が緩和されます。
注意事項:
- 誤差サイズにより、誤差のわずかな影響も減少してしまうことが想定されます。
絶対中央値¶
残差値の中央値。 値が小さいほど誤差が低くなります。
詳細:中央絶対誤差は次のように計算されます。
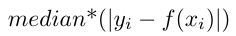
備考
パフォーマンスの理由から、Eureqaモデルでは、(正確な中央値ではなく)推定中央値が使用されます。 小さいデータセットの場合、推定中央値は実際の値と大きく異なることがあります。
使用目的:中央誤差値の最小化。 残差に非常に偏った分布が予期される場合、高いノイズと外れ値の処理に最適です。
注意事項:
- 中央値のいずれかの側の誤差のスケールによる影響はありません。
- 外れ値に対して最も堅牢な誤差指標です。
- 非常に小さいデータセットでは、推定中央値は正確でないことがあります。
四分位平均絶対値¶
残差誤差の四分位範囲(中央の50%)内の絶対誤差の平均。 値が小さいほど誤差が低くなります。
詳細:四分位平均絶対誤差は、残差の中央50%の平均絶対誤差を取ることによって計算されます。
使用目的:中央50%の誤差値の誤差の最小化。 ターゲット特徴量に大きい外れ値が含まれる可能性がある場合、または「平均」パフォーマンスに主に関心がある場合に使用します。 外れ値に対して非常に堅牢であるという点で、中央誤差に似ています。
注意事項:
- 最小および最大誤差は無視されます。
AIC絶対値¶
平均絶対誤差に基づく赤池情報量規準(AIC)。 これは正規化された平均絶対誤差とモデルパラメーターの数に基づくペナルティの組み合わせです。 値が低いほどモデルの品質は高くなります。 その他の誤差指標とは異なり、モデルの精度が高いほどAICは負の無限大に近づく負の値になることがあります。
詳細:AIC絶対誤差は次のように計算されます。
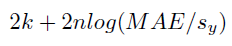
ここでlogは自然対数で、syはターゲット特徴量の標準偏差です。MAEは残差の絶対値の平均です。
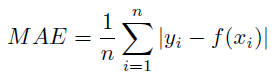
そして、kはモデルに含まれるパラメーターの数です(1の係数を含む条件を含む)。
使用目的: 残差誤差とパラメーターの数の最小化。 この指標では、Loss関数内のパラメーターの数を含めることによって複雑さにペナルティが科せられます。 この指標は、モデル内のパラメーターの数を直接制限してペナルティを科す場合に便利です(物理体形をモデル化する場合や自由パラメーターがほとんどない解が望ましいその他の問題など)。 AIC平均平方誤差指標と似ていますが、外れ値に対する許容度は高くなります。
注意事項:
- この指標を使用する検索で得られる解の数は少なくなり、非常に複雑な解の数が制限されます。
- この指標に最適化することにより、AIC最適化モデルだけが取得されます。
- ノイズは、二重指数分布に従うと仮定されます。
AIC二乗¶
赤池情報量規準(AIC)。 これは正規化された平均平方誤差とモデルパラメーターの数に基づくペナルティの組み合わせです。 値が低いほどモデルの品質は高くなります。 その他の誤差指標とは異なり、モデルの精度が高いほど値は負の無限大に近づく負の値になることがあります。
詳細:AIC平方誤差は次のように計算されます。
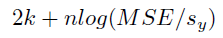
ここでlogは自然対数で、syはターゲット特徴量の標準偏差です。MSEは残差の平方値の平均です。
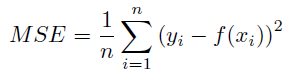
そして、kはモデルに含まれるパラメーターの数です(1の係数を含む条件を含む)。
使用目的:平方残差誤差とパラメーターの数の最小化。 この指標では、Loss関数内のパラメーターの数を含めることによって複雑さにペナルティが科せられます。 この指標は、モデル内のパラメーターの数を直接制限してペナルティを科す場合に便利です(物理体形をモデル化する場合や自由パラメーターがほとんどない解が望ましいその他の問題など)。
注意事項:
- この指標を使用する検索で得られる解の数は少なくなり、非常に複雑な解の数が制限されます。
- この指標に最適化することにより、AIC最適化モデルだけが取得されます。
- 残差は正規分布に従うことが仮定されます。
順位相関(Rank-r)¶
予測値と実測値の順位間の相関係数。 大きい値は強いPositive相関を示します。0は相関がないことを示し、1は完全な順位相関を表します。
詳細:順位相関は予測値の順位と実測値の順位の間の相関係数として計算されます。したがって、出力が順位付けに使用できるモデルが最適化されます。 順位は、それぞれの値を昇順にソートし、ソート位置に基づいて増分値を各行に割り当てることによって計算されます。
使用目的:予測順位と実測順位の間の相関の最大化。 モデルでポイント間の相対的な順序を予測する必要があり、実際の予測値が重要でない場合に使用します。
注意事項:
- 値は、序数、間隔、または割合である必要があります。
- 1の順位相関は2つの特徴量の間に単調な関係性があることを示します。
- データのスケールに関係なく、値は常に[-1,1]のスケール内です。
- 実測値と予測値の範囲が大きく異なる場合、結果のプロットは予期した通りに表示されないことがあります。 たとえば、予測値が(29, 30, 32, 584, 9999, 10000)や(100001, 100002, 100003, 100004, 100005, 100006)である場合、(1, 2, 3, 4, 5, 6)の実測値では、予測値と実測値の順位が同じなので結果は誤差ゼロになります。 しかし、予測値の範囲が非常に広いので、実測値のプロットに表示されないことがあります。
ヒンジ損失¶
分類予測の平均「ヒンジロス」。 ヒンジロスでは、間違った予測の信頼度が高くなるにしたがってペナルティが高くなりますが、真の予測も最小しきい値に達した後は同様に処理されます。 値が小さいほど誤差が低くなります。
詳細:ヒンジロス誤差は次のように計算されます。
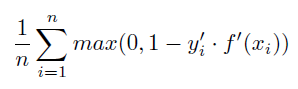
ここで、0として表現される二項クラスと1として表される二項クラスは、それぞれ-1と1に再スケールされます。
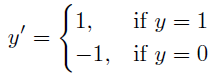
and
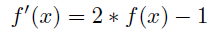
この計算では、予測値f(xi)と実測値yiの符号が同じ(正しい予測)で、予測値が1以上である場合、誤差は0と見なされます。符号が異なる場合(間違った予測)、誤差はf(xi)で線状に増加します。
使用目的:分類誤差の最小化。 ヒンジロス誤差は不均衡な指標で、間違った予測の信頼度が高くなるにしたがってペナルティが高くなりますが、真の予測も最小しきい値に達した後は同様に処理されます。
注意事項:
- 分類問題に使用する場合、ターゲット式にはlogistic()関数を含めないでください。 この誤差指標では、予測値の範囲が広いことが予期されます。
- 予測されたスコアを0または1の予測に変換するとき0.5のしきい値が仮定されます。
スロープ絶対値¶
予測された行ごとのデルタおよび実測の行ごとのデルタの平均絶対誤差。 値が小さいほど誤差が低くなります。
詳細:傾斜絶対誤差は次のように計算されます。
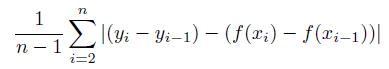
モデル方程式のそれぞれの側(予測値および実測値)に対して、この指標は、各行とその前の行の値の間の行ごとの「デルタ」を計算します。 傾斜絶対誤差は、実測デルタと予測デルタの間の平均絶対誤差です。
使用目的:デルタの誤差の最小化。 1つの期間から次の期間における変化を予測する時系列分析に使用されます。
注意事項:
- これは実験的な(非標準の)誤差指標です。
- データセットの形状に適合します。実際の予測値は実測値と同じ範囲にないことがあります。