Confusion matrix¶
The ROC Curve tab provides a confusion matrix that lets you evaluate accuracy by comparing actual versus predicted values. The confusion matrix is a table that reports true versus predicted values. The name “confusion matrix” is used because the matrix shows whether the model is confusing two classes (consistently mislabeling one class as another class).
The confusion matrix facilitates more detailed analysis than relying on accuracy alone. Accuracy yields misleading results if the dataset is unbalanced (great variation in the number of samples in different classes), so it is not always a reliable metric for the real performance of a classifier.
To evaluate accuracy using the confusion matrix:
-
Select a model on the Leaderboard and navigate to Evaluate > ROC Curve.
-
Select a data source and set the display threshold. The confusion matrix displays on the right side of the ROC Curve tab.
Analyze the confusion matrix¶
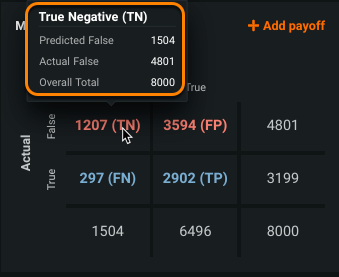
The rows and columns of the confusion matrix below report true and false values of the hospital readmission classification use case.
Note
The Prediction Distribution graph uses these same values and definitions.
-
Each column of the matrix represents the instances in a predicted class (predicted not readmitted, predicted readmitted).
-
Each row represents the instances in an actual class (actually not readmitted, actually readmitted). If you look at the Actual axis on the left in the example above, True corresponds to the blue row and represents the positive class (1 or readmitted), while False corresponds to the red row and represents the negative class (0 or not readmitted).
-
Total correct predictions are comprised of TP + TN; total incorrect predictions are comprised of FP + FN. In the sample matrix above:
Value Model prediction True Negative (TN) 459 patients predicted to not readmit that actually did not readmit. Correctly predicted False when actual was False. False Positive (FP) 506 patients predicted to readmit, but actually did not readmit. Incorrectly predicted True when actual was False. False Negative (FN) 123 patients predicted to not readmit, but actually did readmit. Incorrectly predicted False when actual was True. True Positive (TP) 512 patients predicted to readmit that actually readmitted. Correctly predicted True when actual was True. -
The matrix displays totals by row and column:
-
To view total counts, hover over a cell in the matrix. The tooltip shows the marginal totals (row and column sums) rather than just the individual cell value. In this example, the predicted false values were 459 + 123, even though 123 were actually true. Use these values to help understand the distribution of your data:
-
The key metrics you can derive from the matrix are calculated as follows (and explained here):
Accuracy Calculation Accuracy (459 + 512) ÷ 1600 = 60.7% overall correct predictions. Precision 512 ÷ (512 + 506) = 50.3% of positive predictions were correct. Recall/Sensitivity 512 ÷ (512 + 123) = 80.6% of actual positives were caught. Specificity 459 ÷ (459 + 506) = 47.6% of actual negatives were correctly identified.
Count differences¶
When smart downsampling is enabled, the confusion matrix totals may differ slightly from the size of the data partitions (validation, cross-validation, and holdout). This is largely due to a rounding error. In actuality, rows from the minority class are always assigned a "weight" of 1 (not to be confused with the weight set in Advanced options and therefore never removed during downsampling). Only rows from the majority class get a "weight" greater than 1 and are potentially downsampled.
When you do apply weights in Advanced options (Classic) or as part of advanced experiment setup (NextGen), the counts shown in the confusion matrix do not align with the training set row counts. This is because the Accuracy optimization metric uses the sum of weights. Specifically:
Every cell of the confusion matrix will be the sum of the sample weights in that cell. If no weights are specified, the implied weight is 1, so the sum of the weights is also the count of observations.